Quantum mechanics | Mathematical formulations

Quantum mechanics (QM – also known as quantum physics, or quantum theory) is a branch of physics which deals with physical phenomena at microscopic scales, where the action is on the order of the Planck constant. Quantum mechanics departs from classical mechanics primarily at the quantum realm of atomic and subatomic length scales. Quantum mechanics provides a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. Quantum mechanics is the non-relativistic limit of Quantum Field Theory (QFT), a theory that was developed later that combined Quantum Mechanics with Relativity.
In advanced topics of quantum mechanics, some of these behaviors are macroscopic and emerge at only extreme (i.e., very low or very high) energies or temperatures. The name quantum mechanics derives from the observation that some physical quantities can change only in discrete amounts (Latin quanta), and not in a continuous (cf. analog) way. For example, the angular momentum of an electron bound to an atom or molecule is quantized. In the context of quantum mechanics, the wave–particle duality of energy and matter and the uncertainty principle provide a unified view of the behavior of photons, electrons, and other atomic-scale objects.
The mathematical formulations of quantum mechanics are abstract. A mathematical function known as the wavefunction provides information about the probability amplitude of position, momentum, and other physical properties of a particle. Mathematical manipulations of the wavefunction usually involve the bra-ket notation, which requires an understanding of complex numbers and linear functionals. The wavefunction treats the object as a quantum harmonic oscillator, and the mathematics is akin to that describing acoustic resonance. Many of the results of quantum mechanics are not easily visualized in terms of classical mechanics—for instance, the ground state in a quantum mechanical model is a non-zero energy state that is the lowest permitted energy state of a system, as opposed to a more "traditional" system that is thought of as simply being at rest, with zero kinetic energy. Instead of a traditional static, unchanging zero state, quantum mechanics allows for far more dynamic, chaotic possibilities, according to John Wheeler.
The earliest versions of quantum mechanics were formulated in the first decade of the 20th century. At around the same time, the atomic theory and the corpuscular theory of light (as updated by Einstein) first came to be widely accepted as scientific fact; these latter theories can be viewed as quantum theories of matter and electromagnetic radiation, respectively. Early quantum theory was significantly reformulated in the mid-1920s by Werner Heisenberg, Max Born and Pascual Jordan, who created matrix mechanics; Louis de Broglie and Erwin Schrödinger (Wave Mechanics); and Wolfgang Pauli and Satyendra Nath Bose (statistics of subatomic particles). And the Copenhagen interpretation of Niels Bohr became widely accepted. By 1930, quantum mechanics had been further unified and formalized by the work of David Hilbert, Paul Dirac and John von Neumann, with a greater emphasis placed on measurement in quantum mechanics, the statistical nature of our knowledge of reality, and philosophical speculation about the role of the observer. Quantum mechanics has since branched out into almost every aspect of 20th century physics and other disciplines, such as quantum chemistry, quantum electronics, quantum optics, and quantum information science. Much 19th century physics has been re-evaluated as the "classical limit" of quantum mechanics, and its more advanced developments in terms of quantum field theory, string theory, and speculative quantum gravity theories.

History

Scientific inquiry into the wave nature of light began in the 17th and 18th centuries when scientists such as Robert Hooke, Christian Huygens and Leonhard Euler proposed a wave theory of light based on experimental observations. In 1803, Thomas Young, an English polymath, performed the famous double-slit experiment that he later described in a paper entitled "On the nature of light and colours". This experiment played a major role in the general acceptance of the wave theory of light.
In 1838, with the discovery of cathode rays by Michael Faraday, these studies were followed by the 1859 statement of the black-body radiation problem by Gustav Kirchhoff, the 1877 suggestion by Ludwig Boltzmann that the energy states of a physical system can be discrete, and the 1900 quantum hypothesis of Max Planck.Planck's hypothesis that energy is radiated and absorbed in discrete "quanta" (or "energy elements") precisely matched the observed patterns of black-body radiation.
In 1896, Wilhelm Wien empirically determined a distribution law of black-body radiation, known as Wien's law in his honor. Ludwig Boltzmann independently arrived at this result by considerations of Maxwell's equations. However, it was valid only at high frequencies, and underestimated the radiance at low frequencies. Later, Max Planck corrected this model using Boltzmann statistical interpretation of thermodynamics and proposed what is now called Planck's law, which led to the development of quantum mechanics.

Among the first to study quantum phenomena in nature were Arthur Compton, C.V. Raman, Pieter Zeeman, each of whom has a quantum effect named after him. Robert A. Millikan studied the Photoelectric effect experimentally and Albert Einstein developed a theory for it. At the same time Niels Bohr developed his theory of the atomic structure which was later confirmed by the experiments of Henry Moseley. In 1913, Peter Debye extended Niels Bohr's theory of atomic structure, introducing elliptical orbits, a concept also introduced by Arnold Sommerfeld. This phase is known as Old quantum theory.
According to Planck, each energy element E is proportional to its frequency ν:

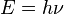
Planck is considered the father of the Quantum Theory:

where h is Planck's constant. Planck (cautiously) insisted that this was simply an aspect of the processes of absorption and emission of radiation and had nothing to do with the physical reality of the radiation itself.In fact, he considered his quantum hypothesis a mathematical trick to get the right answer rather than a sizeable discovery. However, in 1905 Albert Einstein interpreted Planck's quantum hypothesis realistically and used it to explain the photoelectric effect, in which shining light on certain materials can eject electrons from the material.

The foundations of quantum mechanics were established during the first half of the 20th century by Max Planck, Niels Bohr, Werner Heisenberg, Louis de Broglie, Arthur Compton, Albert Einstein, Erwin Schrödinger, Max Born, John von Neumann, Paul Dirac, Enrico Fermi, Wolfgang Pauli, Max von Laue, Freeman Dyson, David Hilbert, Wilhelm Wien, Satyendra Nath Bose, Arnold Sommerfeld and others. In the mid-1920s, developments in quantum mechanics led to its becoming the standard formulation for atomic physics. In the summer of 1925, Bohr and Heisenberg published results that closed the "Old Quantum Theory". Out of deference to their particle-like behavior in certain processes and measurements, light quanta came to be called photons (1926). From Einstein's simple postulation was born a flurry of debating, theorizing, and testing. Thus the entire field of quantum physics emerged, leading to its wider acceptance at the Fifth Solvay Conference in 1927. 

The other exemplar that led to quantum mechanics was the study of electromagnetic waves, such as visible and ultraviolet light. When it was found in 1900 by Max Planck that the energy of waves could be described as consisting of small packets or "quanta", Albert Einstein further developed this idea to show that an electromagnetic wave such as light could also be described as a particle (later called the photon) with a discrete quantum of energy that was dependent on its frequency. As a matter of fact, Einstein was able to use the photon theory of light to explain the photoelectric effect, for which he won the Nobel Prize in 1921. This led to a theory of unity between subatomic particles and electromagnetic waves, called wave–particle duality, in which particles and waves were neither one nor the other, but had certain properties of both. Thus coined the term wave-particle duality.

While quantum mechanics traditionally described the world of the very small, it is also needed to explain certain recently investigated macroscopic systems such as superconductors, superfluids, and larger organic molecules.

The word quantum derives from the Latin, meaning "how great" or "how much". In quantum mechanics, it refers to a discrete unit that quantum theory assigns to certain physical quantities, such as the energy of an atom at rest (see Figure 1). The discovery that particles are discrete packets of energy with wave-like properties led to the branch of physics dealing with atomic and sub-atomic systems which is today called quantum mechanics. It is the underlying mathematical framework of many fields of physics and chemistry, including condensed matter physics, solid-state physics, atomic physics, molecular physics, computational physics, computational chemistry, quantum chemistry, particle physics, nuclear chemistry, and nuclear physics. Some fundamental aspects of the theory are still actively studied.

Quantum mechanics is essential to understanding the behavior of systems at atomic length scales and smaller. In addition, if classical mechanics truly governed the workings of an atom, electrons would really 'orbit' the nucleus. Since bodies in circular motion accelerate, they must emit radiation and collide with the nucleus in the process. This clearly contradicts the existence of stable atoms. However, in the natural world electrons normally remain in an uncertain, non-deterministic, "smeared", probabilistic wave–particle wavefunction orbital path around (or through) the nucleus, defying the traditional assumptions of classical mechanics and electromagnetism.

Quantum mechanics was initially developed to provide a better explanation and description of the atom, especially the differences in the spectra of light emitted by different isotopes of the same element, as well as subatomic particles. In short, the quantum-mechanical atomic model has succeeded spectacularly in the realm where classical mechanics and electromagnetism falter.

Broadly speaking, quantum mechanics incorporates four classes of phenomena for which classical physics cannot account:

• The quantization of certain physical properties
• Wave–particle duality
• The Uncertainty principle
• Quantum entanglement.

Mathematical formulations

In the mathematically rigorous formulation of quantum mechanics developed by Paul Dirac, David Hilbert, John von Neumann, and Hermann Weyl the possible states of a quantum mechanical system are represented by unit vectors (called "state vectors"). Formally, these reside in a complex separable Hilbert space - variously called the "state space" or the "associated Hilbert space" of the system - that is well defined up to a complex number of norm 1 (the phase factor). In other words, the possible states are points in the projective space of a Hilbert space, usually called the complex projective space. The exact nature of this Hilbert space is dependent on the system - for example, the state space for position and momentum states is the space of square-integrable functions, while the state space for the spin of a single proton is just the product of two complex planes. Each observable is represented by a maximally Hermitian (precisely: by a self-adjoint) linear operator acting on the state space. Each eigenstate of an observable corresponds to an eigenvector of the operator, and the associated eigenvalue corresponds to the value of the observable in that eigenstate. If the operator's spectrum is discrete, the observable can attain only those discrete eigenvalues.
In the formalism of quantum mechanics, the state of a system at a given time is described by a complex wave function, also referred to as state vector in a complex vector space. This abstract mathematical object allows for the calculation of probabilities of outcomes of concrete experiments. For example, it allows one to compute the probability of finding an electron in a particular region around the nucleus at a particular time. Contrary to classical mechanics, one can never make simultaneous predictions of conjugate variables, such as position and momentum, with accuracy. For instance, electrons may be considered (to a certain probability) to be located somewhere within a given region of space, but with their exact positions unknown. Contours of constant probability, often referred to as "clouds", may be drawn around the nucleus of an atom to conceptualize where the electron might be located with the most probability. Heisenberg's uncertainty principle quantifies the inability to precisely locate the particle given its conjugate momentum.
According to one interpretation, as the result of a measurement the wave function containing the probability information for a system collapses from a given initial state to a particular eigenstate. The possible results of a measurement are the eigenvalues of the operator representing the observable — which explains the choice of Hermitian operators, for which all the eigenvalues are real. The probability distribution of an observable in a given state can be found by computing the spectral decomposition of the corresponding operator. Heisenberg's uncertainty principle is represented by the statement that the operators corresponding to certain observables do not commute.
The probabilistic nature of quantum mechanics thus stems from the act of measurement. This is one of the most difficult aspects of quantum systems to understand. It was the central topic in the famous Bohr-Einstein debates, in which the two scientists attempted to clarify these fundamental principles by way of thought experiments. In the decades after the formulation of quantum mechanics, the question of what constitutes a "measurement" has been extensively studied. Newer interpretations of quantum mechanics have been formulated that do away with the concept of "wavefunction collapse" (see, for example, the relative state interpretation). The basic idea is that when a quantum system interacts with a measuring apparatus, their respective wavefunctions become entangled, so that the original quantum system ceases to exist as an independent entity. For details, see the article on measurement in quantum mechanics.
Generally, quantum mechanics does not assign definite values. Instead, it makes a prediction using a probability distribution; that is, it describes the probability of obtaining the possible outcomes from measuring an observable. Often these results are skewed by many causes, such as dense probability clouds. Probability clouds are approximate, but better than the Bohr model, whereby electron location is given by a probability function, the wave function eigenvalue, such that the probability is the squared modulus of the complex amplitude, or quantum state nuclear attraction. Naturally, these probabilities will depend on the quantum state at the "instant" of the measurement. Hence, uncertainty is involved in the value. There are, however, certain states that are associated with a definite value of a particular observable. These are known as eigenstates of the observable ("eigen" can be translated from German as meaning "inherent" or "characteristic").
In the everyday world, it is natural and intuitive to think of everything (every observable) as being in an eigenstate. Everything appears to have a definite position, a definite momentum, a definite energy, and a definite time of occurrence. However, quantum mechanics does not pinpoint the exact values of a particle's position and momentum (since they are conjugate pairs) or its energy and time (since they too are conjugate pairs); rather, it provides only a range of probabilities in which that particle might be given its momentum and momentum probability. Therefore, it is helpful to use different words to describe states having uncertain values and states having definite values (eigenstates). Usually, a system will not be in an eigenstate of the observable (particle) we are interested in. However, if one measures the observable, the wavefunction will instantaneously be an eigenstate (or "generalized" eigenstate) of that observable. This process is known as wavefunction collapse, a controversial and much-debated process that involves expanding the system under study to include the measurement device. If one knows the corresponding wave function at the instant before the measurement, one will be able to compute the probability of the wavefunction collapsing into each of the possible eigenstates. For example, the free particle in the previous example will usually have a wavefunction that is a wave packet centered around some mean position x₀ (neither an eigenstate of position nor of momentum). When one measures the position of the particle, it is impossible to predict with certainty the result. It is probable, but not certain, that it will be near x₀, where the amplitude of the wave function is large. After the measurement is performed, having obtained some result x, the wave function collapses into a position eigenstate centered at x.
The time evolution of a quantum state is described by the Schrödinger equation, in which the Hamiltonian (the operator corresponding to the total energy of the system) generates the time evolution. The time evolution of wave functions is deterministic in the sense that - given a wavefunction at an initial time - it makes a definite prediction of what the wavefunction will be at any later time.
During a measurement, on the other hand, the change of the initial wavefunction into another, later wavefunction is not deterministic, it is unpredictable (i.e., random). A time-evolution simulation can be seen here.
Wave functions change as time progresses. The Schrödinger equation describes how wavefunctions change in time, playing a role similar to Newton's second law in classical mechanics. The Schrödinger equation, applied to the aforementioned example of the free particle, predicts that the center of a wave packet will move through space at a constant velocity (like a classical particle with no forces acting on it). However, the wave packet will also spread out as time progresses, which means that the position becomes more uncertain with time. This also has the effect of turning a position eigenstate (which can be thought of as an infinitely sharp wave packet) into a broadened wave packet that no longer represents a (definite, certain) position eigenstate.