Atomic Talbot effect | Talbot effect

The Talbot effect is a near-field diffraction effect first observed in 1836 by Henry Fox Talbot. When a plane wave is incident upon a periodic diffraction grating, the image of the grating is repeated at regular distances away from the grating plane. The regular distance is called the Talbot length, and the repeated images are called self images or Talbot images. Furthermore, at half the Talbot length, a self image also occurs, but phase-shifted by half a period (the physical meaning of this is that it is laterally shifted by half the width of the grating period). At smaller regular fractions of the Talbot length, sub-images can also be observed. At one quarter of the Talbot length, the self image is halved in size, and appears with half the period of the grating (thus twice as many images are seen). At one eighth of the Talbot length, the period and size of the images is halved again, and so forth creating a fractal pattern of sub images with ever decreasing size, often referred to as a Talbot carpet.
Lord Rayleigh showed that the Talbot effect was a natural consequence of Fresnel diffraction and that the Talbot length can be found by the following formula

where  is the period of the
diffraction grating and
is the period of the
diffraction grating and  is the wavelength of
the light incident on the grating. However, if wavelength
is the wavelength of
the light incident on the grating. However, if wavelength  is comparable to
grating period
is comparable to
grating period  this expression may lead to
errors in
this expression may lead to
errors in  up to 100%. In this case
exact expression derived by Lord Rayleigh should be used
up to 100%. In this case
exact expression derived by Lord Rayleigh should be used
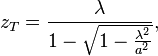
The
atomic Talbot effect
Due to the quantum
mechanical wave nature of particles, diffraction effects have also been
observed with atoms—effects which are similar to those in the case of light.
Chapman et al. carried out an experiment in which a collimated beam of sodium
atoms was passed through two diffraction gratings (the second used as a mask)
to observe the Talbot effect and measure the Talbot length. The
beam had a mean velocity of 1000 m/s corresponding to
a de Broglie wavelength of  = 0.017 nm. Their experiment was performed with 200 and 300 nm gratings which yielded Talbot lengths of 4.7 and 10.6 mm respectively. This showed that for an atomic beam
of constant velocity, by using
= 0.017 nm. Their experiment was performed with 200 and 300 nm gratings which yielded Talbot lengths of 4.7 and 10.6 mm respectively. This showed that for an atomic beam
of constant velocity, by using  , the atomic
Talbot length can be found in the same manner.
, the atomic
Talbot length can be found in the same manner.
 = 0.017 nm. Their experiment was performed with 200 and 300 nm gratings which yielded Talbot lengths of 4.7 and 10.6 mm respectively. This showed that for an atomic beam
of constant velocity, by using
= 0.017 nm. Their experiment was performed with 200 and 300 nm gratings which yielded Talbot lengths of 4.7 and 10.6 mm respectively. This showed that for an atomic beam
of constant velocity, by using  , the atomic
Talbot length can be found in the same manner.
, the atomic
Talbot length can be found in the same manner.


